TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI
TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.
FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x [EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG
XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli + DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
número atômico, estrutura eletrônica, níveis de energia - TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- T l T l E l Fl dfG l
X [ESTADO QUÂNTICO]
XTODA FORMA DE FUNÇÃO E EQUAÇÃO EM=
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
Correlação angular perturbada
A correlação angular γ-γ perturbada , PAC para abreviar ou PAC-espectroscopia , é um método de física de estado sólido nuclear com o qual os campos magnéticos e elétricos em estruturas cristalinas podem ser medidos. Ao fazer isso, gradientes de campo elétrico e a frequência de Larmor em campos magnéticos, bem como efeitos dinâmicos, são determinados. Com este método muito sensível, que requer apenas cerca de 10-1000 bilhões de átomos de um isótopo radioativo por medição, as propriedades do material na estrutura local, transições de fase, magnetismo e difusão podem ser investigados. O método PAC está relacionado à ressonância magnética nuclear e ao efeito Mössbauer, mas não apresenta atenuação de sinal em temperaturas muito altas. Hoje, apenas a correlação angular perturbada com diferencial de tempo ( TDPAC ) é usada.
A correlação angular γ-γ perturbada , PAC para abreviar ou PAC-espectroscopia , é um método de física de estado sólido nuclear com o qual os campos magnéticos e elétricos em estruturas cristalinas podem ser medidos. Ao fazer isso, gradientes de campo elétrico e a frequência de Larmor em campos magnéticos, bem como efeitos dinâmicos, são determinados. Com este método muito sensível, que requer apenas cerca de 10-1000 bilhões de átomos de um isótopo radioativo por medição, as propriedades do material na estrutura local, transições de fase, magnetismo e difusão podem ser investigados. O método PAC está relacionado à ressonância magnética nuclear e ao efeito Mössbauer, mas não apresenta atenuação de sinal em temperaturas muito altas. Hoje, apenas a correlação angular perturbada com diferencial de tempo ( TDPAC ) é usada.
Conteúdo
História e Desenvolvimento [ editar ]
PAC remonta a um trabalho teórico de Donald R. Hamilton [1] de 1940. O primeiro experimento bem-sucedido foi realizado por Brady e Deutsch [2] em 1947. Essencialmente, o spin e a paridade dos spins nucleares foram investigados nesses primeiros experimentos de PAC. No entanto, foi reconhecido desde o início que os campos elétricos e magnéticos interagem com o momento nuclear, [3] fornecendo a base para uma nova forma de investigação de materiais: a espectroscopia de estado sólido nuclear.
Passo a passo, a teoria foi desenvolvida. [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] Depois de Abragam e Pound [18]publicaram seu trabalho sobre a teoria do PAC em 1953 incluindo campos nucleares extras, muitos estudos com o PAC foram realizados posteriormente. Nas décadas de 1960 e 1970, o interesse pelos experimentos de PAC aumentou drasticamente, concentrando-se principalmente nos campos magnéticos e elétricos em cristais nos quais os núcleos das sondas foram introduzidos. Em meados da década de 1960, a implantação de íons foi descoberta, proporcionando novas oportunidades para a preparação de amostras. O rápido desenvolvimento eletrônico da década de 1970 trouxe melhorias significativas no processamento de sinais. Da década de 1980 até a atualidade, o PAC surgiu como um importante método de estudo e caracterização de materiais. [19] [20] [21] [22] [23]B. para o estudo de materiais semicondutores, compostos intermetálicos, superfícies e interfaces. Lars Hemmingsen et al. Recentemente, o PAC também foi aplicado em sistemas biológicos. [24]
Enquanto até cerca de 2008 os instrumentos do PAC usavam eletrônicos convencionais de alta frequência da década de 1970, em 2008 Christian Herden e Jens Röder et al. desenvolveu o primeiro instrumento PAC totalmente digitalizado que permite ampla análise de dados e uso paralelo de várias sondas. [25] Réplicas e novos desenvolvimentos se seguiram. [26] [27]
PAC remonta a um trabalho teórico de Donald R. Hamilton [1] de 1940. O primeiro experimento bem-sucedido foi realizado por Brady e Deutsch [2] em 1947. Essencialmente, o spin e a paridade dos spins nucleares foram investigados nesses primeiros experimentos de PAC. No entanto, foi reconhecido desde o início que os campos elétricos e magnéticos interagem com o momento nuclear, [3] fornecendo a base para uma nova forma de investigação de materiais: a espectroscopia de estado sólido nuclear.
Passo a passo, a teoria foi desenvolvida. [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] Depois de Abragam e Pound [18]publicaram seu trabalho sobre a teoria do PAC em 1953 incluindo campos nucleares extras, muitos estudos com o PAC foram realizados posteriormente. Nas décadas de 1960 e 1970, o interesse pelos experimentos de PAC aumentou drasticamente, concentrando-se principalmente nos campos magnéticos e elétricos em cristais nos quais os núcleos das sondas foram introduzidos. Em meados da década de 1960, a implantação de íons foi descoberta, proporcionando novas oportunidades para a preparação de amostras. O rápido desenvolvimento eletrônico da década de 1970 trouxe melhorias significativas no processamento de sinais. Da década de 1980 até a atualidade, o PAC surgiu como um importante método de estudo e caracterização de materiais. [19] [20] [21] [22] [23]B. para o estudo de materiais semicondutores, compostos intermetálicos, superfícies e interfaces. Lars Hemmingsen et al. Recentemente, o PAC também foi aplicado em sistemas biológicos. [24]
Enquanto até cerca de 2008 os instrumentos do PAC usavam eletrônicos convencionais de alta frequência da década de 1970, em 2008 Christian Herden e Jens Röder et al. desenvolveu o primeiro instrumento PAC totalmente digitalizado que permite ampla análise de dados e uso paralelo de várias sondas. [25] Réplicas e novos desenvolvimentos se seguiram. [26] [27]
Princípio de medição [ editar ]
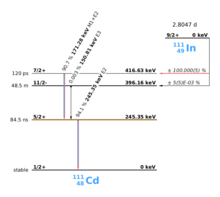
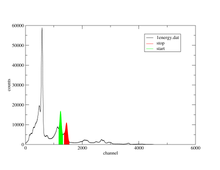
O PAC usa sondas radioativas, que têm um estado intermediário com tempos de decaimento de 2 ns a aprox. 10 μs, consulte o exemplo 111 In na imagem à direita. Após a captura de elétrons (CE), o índio se transmuta em cádmio. Imediatamente depois disso, o núcleo de cádmio 111 está predominantemente no spin nuclear 7/2 + excitado e apenas em uma extensão muito pequena no spin nuclear 11 / 2-, o último não deve ser considerado mais. O estado 7/2 + excitado faz a transição para o estado intermediário 5/2 + emitindo um quantum γ de 171 keV. O estado intermediário tem um tempo de vida de 84,5 ns e é o estado sensível para o PAC. Este estado, por sua vez, decai para o estado fundamental 1/2 + emitindo um quantum γ com 245 keV. O PAC agora detecta os γ-quanta e avalia o primeiro como um sinal de início, o segundo como um sinal de parada.
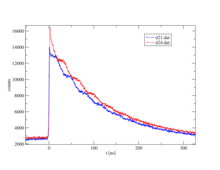
Agora, mede-se o tempo entre o início e a parada de cada evento. Isso é chamado de coincidência quando um par inicial e final é encontrado. Como o estado intermediário decai de acordo com as leis do decaimento radioativo, obtém-se uma curva exponencial com o tempo de vida desse estado intermediário após traçar a frequência ao longo do tempo. Devido à radiação não esférica simétrica do segundo γ-quantum, a chamada anisotropia, que é uma propriedade intrínseca do núcleo nesta transição, ela chega com os campos elétricos e / ou magnéticos circundantes a um distúrbio periódico ( hiperfino interação) A ilustração dos espectros individuais à direita mostra o efeito dessa perturbação como um padrão de onda no decaimento exponencial de dois detectores, um par a 90 ° e outro a 180 ° entre si. As formas de onda de ambos os pares de detectores são alteradas uma da outra. Muito simplesmente, pode-se imaginar um observador fixo olhando para um farol cuja intensidade de luz torna-se periodicamente mais clara e mais escura. Correspondentemente, um arranjo de detector, geralmente quatro detectores em um arranjo planar de 90 ° ou seis detectores em um arranjo octaédrico, "vê" a rotação do núcleo na ordem de magnitude de MHz a GHz.
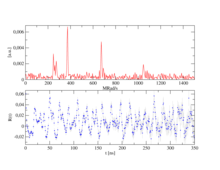
De acordo com o número n de detectores, o número de espectros individuais (z) resulta após z = n²-n, para n = 4, portanto, 12 e para n = 6, portanto, 30. Para obter um espectro de PAC, o 90 ° e Espectros únicos de 180 ° são calculados de forma que as funções exponenciais se cancelem e, além disso, as diferentes propriedades do detector se encurtem. A função de perturbação pura permanece, como mostrado no exemplo de um espectro complexo do PAC. Sua transformada de Fourier fornece as frequências de transição como picos.
, a razão da taxa de contagem, é obtida a partir do espectro único usando:
Dependendo do spin do estado intermediário, um número diferente de frequências de transição aparece. Para 5/2 spin, 3 frequências de transição podem ser observadas com a razão ω 1 + ω 2 = ω 3 . Como regra, uma combinação diferente de 3 frequências pode ser observada para cada local associado na célula unitária.
PAC é um método estatístico: cada átomo sonda radioativa fica em seu próprio ambiente. Nos cristais, devido à alta regularidade do arranjo dos átomos ou íons, os ambientes são idênticos ou muito semelhantes, de modo que as sondas em locais de rede idênticos experimentam o mesmo campo hiperfino ou campo magnético, que então se torna mensurável em um espectro de PAC. Por outro lado, para sondas em ambientes muito diferentes, como em materiais amorfos, geralmente é observada uma ampla distribuição de frequência ou não e o espectro do PAC parece plano, sem resposta de frequência. Com cristais únicos, dependendo da orientação do cristal para os detectores, certas frequências de transição podem ser reduzidas ou extintas, como pode ser visto no exemplo do espectro de PAC do óxido de zinco (ZnO).
O PAC usa sondas radioativas, que têm um estado intermediário com tempos de decaimento de 2 ns a aprox. 10 μs, consulte o exemplo 111 In na imagem à direita. Após a captura de elétrons (CE), o índio se transmuta em cádmio. Imediatamente depois disso, o núcleo de cádmio 111 está predominantemente no spin nuclear 7/2 + excitado e apenas em uma extensão muito pequena no spin nuclear 11 / 2-, o último não deve ser considerado mais. O estado 7/2 + excitado faz a transição para o estado intermediário 5/2 + emitindo um quantum γ de 171 keV. O estado intermediário tem um tempo de vida de 84,5 ns e é o estado sensível para o PAC. Este estado, por sua vez, decai para o estado fundamental 1/2 + emitindo um quantum γ com 245 keV. O PAC agora detecta os γ-quanta e avalia o primeiro como um sinal de início, o segundo como um sinal de parada.
Agora, mede-se o tempo entre o início e a parada de cada evento. Isso é chamado de coincidência quando um par inicial e final é encontrado. Como o estado intermediário decai de acordo com as leis do decaimento radioativo, obtém-se uma curva exponencial com o tempo de vida desse estado intermediário após traçar a frequência ao longo do tempo. Devido à radiação não esférica simétrica do segundo γ-quantum, a chamada anisotropia, que é uma propriedade intrínseca do núcleo nesta transição, ela chega com os campos elétricos e / ou magnéticos circundantes a um distúrbio periódico ( hiperfino interação) A ilustração dos espectros individuais à direita mostra o efeito dessa perturbação como um padrão de onda no decaimento exponencial de dois detectores, um par a 90 ° e outro a 180 ° entre si. As formas de onda de ambos os pares de detectores são alteradas uma da outra. Muito simplesmente, pode-se imaginar um observador fixo olhando para um farol cuja intensidade de luz torna-se periodicamente mais clara e mais escura. Correspondentemente, um arranjo de detector, geralmente quatro detectores em um arranjo planar de 90 ° ou seis detectores em um arranjo octaédrico, "vê" a rotação do núcleo na ordem de magnitude de MHz a GHz.
De acordo com o número n de detectores, o número de espectros individuais (z) resulta após z = n²-n, para n = 4, portanto, 12 e para n = 6, portanto, 30. Para obter um espectro de PAC, o 90 ° e Espectros únicos de 180 ° são calculados de forma que as funções exponenciais se cancelem e, além disso, as diferentes propriedades do detector se encurtem. A função de perturbação pura permanece, como mostrado no exemplo de um espectro complexo do PAC. Sua transformada de Fourier fornece as frequências de transição como picos.
, a razão da taxa de contagem, é obtida a partir do espectro único usando:
Dependendo do spin do estado intermediário, um número diferente de frequências de transição aparece. Para 5/2 spin, 3 frequências de transição podem ser observadas com a razão ω 1 + ω 2 = ω 3 . Como regra, uma combinação diferente de 3 frequências pode ser observada para cada local associado na célula unitária.
PAC é um método estatístico: cada átomo sonda radioativa fica em seu próprio ambiente. Nos cristais, devido à alta regularidade do arranjo dos átomos ou íons, os ambientes são idênticos ou muito semelhantes, de modo que as sondas em locais de rede idênticos experimentam o mesmo campo hiperfino ou campo magnético, que então se torna mensurável em um espectro de PAC. Por outro lado, para sondas em ambientes muito diferentes, como em materiais amorfos, geralmente é observada uma ampla distribuição de frequência ou não e o espectro do PAC parece plano, sem resposta de frequência. Com cristais únicos, dependendo da orientação do cristal para os detectores, certas frequências de transição podem ser reduzidas ou extintas, como pode ser visto no exemplo do espectro de PAC do óxido de zinco (ZnO).
Configuração Instrumental [ editar ]
No espectrômetro PAC típico, uma configuração de quatro detectores de matriz planar de 90 ° e 180 ° ou seis detectores de matriz octaédrica são colocados em torno da amostra da fonte radioativa. Os detectores usados são cristais de cintilação de BaF 2 ou NaI. Para instrumentos modernos hoje, principalmente LaBr 3 : Ce ou CeBr 3são usados. Os fotomultiplicadores convertem os fracos flashes de luz em sinais elétricos gerados no cintilador por radiação gama. Em instrumentos clássicos, esses sinais são amplificados e processados em circuitos lógicos AND / OR em combinação com janelas de tempo das diferentes combinações de detectores (para 4 detectores: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42 , 43) atribuídos e contados. Os espectrômetros digitais modernos usam cartões digitalizadores que usam diretamente o sinal e os convertem em valores de energia e tempo e os armazenam em discos rígidos. Em seguida, eles são pesquisados pelo software em busca de coincidências. Enquanto em instrumentos clássicos, "janelas" que limitam as respectivas energias γ devem ser definidas antes do processamento, isso não é necessário para o PAC digital durante o registro da medição. A análise ocorre apenas na segunda etapa. No caso de sondas com cascatas complexas, isso permite realizar uma otimização dos dados ou avaliar várias cascatas em paralelo, bem como medir diferentes sondas simultaneamente. Os volumes de dados resultantes podem ser entre 60 e 300 GB por medição.
No espectrômetro PAC típico, uma configuração de quatro detectores de matriz planar de 90 ° e 180 ° ou seis detectores de matriz octaédrica são colocados em torno da amostra da fonte radioativa. Os detectores usados são cristais de cintilação de BaF 2 ou NaI. Para instrumentos modernos hoje, principalmente LaBr 3 : Ce ou CeBr 3são usados. Os fotomultiplicadores convertem os fracos flashes de luz em sinais elétricos gerados no cintilador por radiação gama. Em instrumentos clássicos, esses sinais são amplificados e processados em circuitos lógicos AND / OR em combinação com janelas de tempo das diferentes combinações de detectores (para 4 detectores: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42 , 43) atribuídos e contados. Os espectrômetros digitais modernos usam cartões digitalizadores que usam diretamente o sinal e os convertem em valores de energia e tempo e os armazenam em discos rígidos. Em seguida, eles são pesquisados pelo software em busca de coincidências. Enquanto em instrumentos clássicos, "janelas" que limitam as respectivas energias γ devem ser definidas antes do processamento, isso não é necessário para o PAC digital durante o registro da medição. A análise ocorre apenas na segunda etapa. No caso de sondas com cascatas complexas, isso permite realizar uma otimização dos dados ou avaliar várias cascatas em paralelo, bem como medir diferentes sondas simultaneamente. Os volumes de dados resultantes podem ser entre 60 e 300 GB por medição.
Materiais de amostra [ editar ]
Como materiais para a investigação (amostras) são, em princípio, todos os materiais que podem ser sólidos e líquidos. Dependendo da questão e do objetivo da investigação, surgem certas condições de enquadramento. Para a observação de freqüências de perturbação claras é necessário, devido ao método estatístico, que uma certa proporção dos átomos da sonda estejam em um ambiente semelhante e, por exemplo, experimentem o mesmo gradiente de campo elétrico. Além disso, durante a janela de tempo entre o início e a parada, ou aproximadamente 5 meias-vidas do estado intermediário, a direção do gradiente do campo elétrico não deve mudar. Em líquidos, portanto, nenhuma frequência de interferência pode ser medida como resultado das colisões frequentes, a menos que a sonda seja complexada em moléculas grandes, como nas proteínas.
Os materiais mais estudados com PAC são sólidos como semicondutores, metais, isoladores e vários tipos de materiais funcionais. Para as investigações, geralmente são cristalinos. Os materiais amorfos não possuem estruturas altamente ordenadas. No entanto, eles estão próximos, o que pode ser visto na espectroscopia do PAC como uma ampla distribuição de frequências. Os nanomateriais têm um núcleo cristalino e uma concha que tem uma estrutura bastante amorfa. Isso é chamado de modelo core-shell. Quanto menor for a nanopartícula, maior será a fração de volume dessa porção amorfa. Nas medições de PAC, isso é mostrado pela diminuição do componente de frequência cristalina em uma redução da amplitude (atenuação).
Como materiais para a investigação (amostras) são, em princípio, todos os materiais que podem ser sólidos e líquidos. Dependendo da questão e do objetivo da investigação, surgem certas condições de enquadramento. Para a observação de freqüências de perturbação claras é necessário, devido ao método estatístico, que uma certa proporção dos átomos da sonda estejam em um ambiente semelhante e, por exemplo, experimentem o mesmo gradiente de campo elétrico. Além disso, durante a janela de tempo entre o início e a parada, ou aproximadamente 5 meias-vidas do estado intermediário, a direção do gradiente do campo elétrico não deve mudar. Em líquidos, portanto, nenhuma frequência de interferência pode ser medida como resultado das colisões frequentes, a menos que a sonda seja complexada em moléculas grandes, como nas proteínas.
Os materiais mais estudados com PAC são sólidos como semicondutores, metais, isoladores e vários tipos de materiais funcionais. Para as investigações, geralmente são cristalinos. Os materiais amorfos não possuem estruturas altamente ordenadas. No entanto, eles estão próximos, o que pode ser visto na espectroscopia do PAC como uma ampla distribuição de frequências. Os nanomateriais têm um núcleo cristalino e uma concha que tem uma estrutura bastante amorfa. Isso é chamado de modelo core-shell. Quanto menor for a nanopartícula, maior será a fração de volume dessa porção amorfa. Nas medições de PAC, isso é mostrado pela diminuição do componente de frequência cristalina em uma redução da amplitude (atenuação).
A preparação da amostra [ editar ]
A quantidade de isótopos PAC adequados necessários para uma medição está entre cerca de 10 a 1000 bilhões de átomos (10 10 -10 12 ). A quantidade certa depende das propriedades particulares do isótopo. 10 bilhões de átomos são uma quantidade muito pequena de substância. Para comparação, um mol contém cerca de 6,22x10 23 partículas. 10 12 átomos em um centímetro cúbico de berílio dão uma concentração de cerca de 8 nmol / L (nanomol = 10 −9 mol). Cada uma das amostras radioativas tem uma atividade de 0,1-5 MBq, que está na ordem do limite de isenção para o respectivo isótopo.
A forma como os isótopos PAC são trazidos para a amostra a ser examinada depende do experimentador e das possibilidades técnicas. Os seguintes métodos são usuais:
A quantidade de isótopos PAC adequados necessários para uma medição está entre cerca de 10 a 1000 bilhões de átomos (10 10 -10 12 ). A quantidade certa depende das propriedades particulares do isótopo. 10 bilhões de átomos são uma quantidade muito pequena de substância. Para comparação, um mol contém cerca de 6,22x10 23 partículas. 10 12 átomos em um centímetro cúbico de berílio dão uma concentração de cerca de 8 nmol / L (nanomol = 10 −9 mol). Cada uma das amostras radioativas tem uma atividade de 0,1-5 MBq, que está na ordem do limite de isenção para o respectivo isótopo.
A forma como os isótopos PAC são trazidos para a amostra a ser examinada depende do experimentador e das possibilidades técnicas. Os seguintes métodos são usuais:
Implantação [ editar ]
Durante a implantação, um feixe de íons radioativos é gerado, o qual é direcionado para o material da amostra. Devido à energia cinética dos íons (1-500 keV), eles voam para a rede cristalina e são retardados por impactos. Eles param em locais intersticiais ou empurram um átomo de rede para fora de seu lugar e o substituem. Isso leva a uma ruptura da estrutura cristalina. Esses distúrbios podem ser investigados com PAC. Ao moderar, esses distúrbios podem ser curados. Se, por outro lado, os defeitos de radiação no cristal e sua cura devem ser examinados, amostras não percebidas são medidas, que são então recozidas passo a passo.
O implante geralmente é o método de escolha, pois pode ser usado para produzir amostras muito bem definidas.
Durante a implantação, um feixe de íons radioativos é gerado, o qual é direcionado para o material da amostra. Devido à energia cinética dos íons (1-500 keV), eles voam para a rede cristalina e são retardados por impactos. Eles param em locais intersticiais ou empurram um átomo de rede para fora de seu lugar e o substituem. Isso leva a uma ruptura da estrutura cristalina. Esses distúrbios podem ser investigados com PAC. Ao moderar, esses distúrbios podem ser curados. Se, por outro lado, os defeitos de radiação no cristal e sua cura devem ser examinados, amostras não percebidas são medidas, que são então recozidas passo a passo.
O implante geralmente é o método de escolha, pois pode ser usado para produzir amostras muito bem definidas.
A evaporação [ editar ]
No vácuo, a sonda PAC pode ser evaporada na amostra. A sonda radioativa é aplicada a uma placa quente ou filamento, onde é levada à temperatura de evaporação e condensada no material de amostra oposto. Com este método, por exemplo, as superfícies são examinadas. Além disso, por deposição de vapor de outros materiais, interfaces podem ser produzidas. Eles podem ser estudados durante o revenimento com PAC e suas alterações podem ser observadas. Da mesma forma, a sonda PAC pode ser transferida para pulverização catódica usando um plasma.
No vácuo, a sonda PAC pode ser evaporada na amostra. A sonda radioativa é aplicada a uma placa quente ou filamento, onde é levada à temperatura de evaporação e condensada no material de amostra oposto. Com este método, por exemplo, as superfícies são examinadas. Além disso, por deposição de vapor de outros materiais, interfaces podem ser produzidas. Eles podem ser estudados durante o revenimento com PAC e suas alterações podem ser observadas. Da mesma forma, a sonda PAC pode ser transferida para pulverização catódica usando um plasma.
Difusão [ editar ]
No método de difusão, a sonda radioativa é geralmente diluída em um solvente aplicado à amostra, seca e é difundida no material por meio de têmpera. A solução com a sonda radioativa deve ser o mais pura possível, uma vez que todas as outras substâncias podem se difundir na amostra e, assim, afetar os resultados da medição. A amostra deve ser suficientemente diluída na amostra. Portanto, o processo de difusão deve ser planejado de forma que uma distribuição uniforme ou profundidade de penetração suficiente seja alcançada.
No método de difusão, a sonda radioativa é geralmente diluída em um solvente aplicado à amostra, seca e é difundida no material por meio de têmpera. A solução com a sonda radioativa deve ser o mais pura possível, uma vez que todas as outras substâncias podem se difundir na amostra e, assim, afetar os resultados da medição. A amostra deve ser suficientemente diluída na amostra. Portanto, o processo de difusão deve ser planejado de forma que uma distribuição uniforme ou profundidade de penetração suficiente seja alcançada.
Adicionado durante a síntese [ editar ]
Sondas de PAC também podem ser adicionadas durante a síntese de materiais de amostra para alcançar a distribuição mais uniforme na amostra. Este método é particularmente adequado se, por exemplo, a sonda PAC difunde-se apenas mal no material e uma concentração mais alta nos contornos de grão é esperada. Uma vez que apenas amostras muito pequenas são necessárias com PAC (cerca de 5 mm), micro-reatores podem ser usados. Idealmente, a sonda é adicionada à fase líquida do processo sol-gel ou a uma das fases precursoras posteriores.
Sondas de PAC também podem ser adicionadas durante a síntese de materiais de amostra para alcançar a distribuição mais uniforme na amostra. Este método é particularmente adequado se, por exemplo, a sonda PAC difunde-se apenas mal no material e uma concentração mais alta nos contornos de grão é esperada. Uma vez que apenas amostras muito pequenas são necessárias com PAC (cerca de 5 mm), micro-reatores podem ser usados. Idealmente, a sonda é adicionada à fase líquida do processo sol-gel ou a uma das fases precursoras posteriores.
Activação de neutrões [ editar ]
Na ativação de nêutrons , a sonda é preparada diretamente do material da amostra, convertendo uma parte muito pequena de um dos elementos do material da amostra na sonda PAC desejada ou seu isótopo pai por captura de nêutrons. Tal como acontece com a implantação, os danos por radiação devem ser curados. Este método é limitado a materiais de amostra contendo elementos a partir dos quais podem ser feitas sondas PAC de captura de nêutrons. Além disso, as amostras podem ser contaminadas intencionalmente com os elementos que devem ser ativados. Por exemplo, o háfnio é perfeitamente adequado para ativação devido à sua grande seção transversal de captura de nêutrons.
Na ativação de nêutrons , a sonda é preparada diretamente do material da amostra, convertendo uma parte muito pequena de um dos elementos do material da amostra na sonda PAC desejada ou seu isótopo pai por captura de nêutrons. Tal como acontece com a implantação, os danos por radiação devem ser curados. Este método é limitado a materiais de amostra contendo elementos a partir dos quais podem ser feitas sondas PAC de captura de nêutrons. Além disso, as amostras podem ser contaminadas intencionalmente com os elementos que devem ser ativados. Por exemplo, o háfnio é perfeitamente adequado para ativação devido à sua grande seção transversal de captura de nêutrons.
Reação nuclear [ editar ]
Raramente usados são reações nucleares diretas nas quais os núcleos são convertidos em sondas PAC por bombardeio por partículas elementares de alta energia ou prótons. Isso causa grandes danos de radiação, que devem ser curados. Este método é usado com PAD, que pertence aos métodos PAC.
Raramente usados são reações nucleares diretas nas quais os núcleos são convertidos em sondas PAC por bombardeio por partículas elementares de alta energia ou prótons. Isso causa grandes danos de radiação, que devem ser curados. Este método é usado com PAD, que pertence aos métodos PAC.
Laboratories [ editar ]
O maior laboratório de PAC do mundo atualmente está localizado no ISOLDE no CERN com cerca de 10 instrumentos de PAC, que recebe seu principal financiamento do BMBF . Feixes de íons radioativos são produzidos no ISOLDE bombardeando prótons do impulsionador em materiais alvo (carboneto de urânio, estanho líquido, etc.) e evaporando os produtos de fragmentação em altas temperaturas (até 2.000 ° C), ionizando-os e então acelerando-os . Com a separação de massa subsequente, geralmente podem ser produzidos feixes de isótopos muito puros, que podem ser implantados em amostras de PAC. De particular interesse para o PAC são as sondas isoméricas de vida curta, tais como: 111m Cd, 199m Hg, 204m Pb e várias sondas de terras raras.
O maior laboratório de PAC do mundo atualmente está localizado no ISOLDE no CERN com cerca de 10 instrumentos de PAC, que recebe seu principal financiamento do BMBF . Feixes de íons radioativos são produzidos no ISOLDE bombardeando prótons do impulsionador em materiais alvo (carboneto de urânio, estanho líquido, etc.) e evaporando os produtos de fragmentação em altas temperaturas (até 2.000 ° C), ionizando-os e então acelerando-os . Com a separação de massa subsequente, geralmente podem ser produzidos feixes de isótopos muito puros, que podem ser implantados em amostras de PAC. De particular interesse para o PAC são as sondas isoméricas de vida curta, tais como: 111m Cd, 199m Hg, 204m Pb e várias sondas de terras raras.
Teoria [ editar ]
O primeiro -quantum () será emitido isotopicamente. A detecção desse quantum em um detector seleciona um subconjunto com uma orientação das muitas direções possíveis que tem um dado. O segundo-quantum () tem uma emissão anisotrópica e mostra o efeito da correlação angular. O objetivo é medir a probabilidade relativa com a detecção de no ângulo fixo em relação a . A probabilidade é dada com a correlação do ângulo ( teoria das perturbações ):
Para --cascata, é devido à preservação da paridade :
Onde é o spin do estado intermediário e com a multipolaridade [ desambiguação necessária ] das duas transições. Para transições multipolares puras, é.
é o coeficiente de anisotropia que depende do momento angular do estado intermediário e das multipolaridades da transição.
O núcleo radioativo é construído no material da amostra e emite dois -quanta após a decadência. Durante a vida do estado intermediário, ou seja, o tempo entre e , o núcleo sofre uma perturbação devido à interação hiperfina por meio de seu ambiente elétrico e magnético. Este distúrbio muda a correlação angular para:
é o fator de perturbação. Devido à interação elétrica e magnética, o momento angular do estado intermediárioexperimenta um torque em torno de seu eixo de simetria. Mecanicamente quântico, isso significa que a interação leva a transições entre os M estados. O segundo-quantum () é então enviado do nível intermediário. Essa mudança populacional é a razão para a atenuação da correlação.
A interação ocorre entre o momento dipolar do núcleo magnético e o estado intermediário ou / e um campo magnético externo . A interação também ocorre entre o momento quadrupolo nuclear e o gradiente de campo elétrico fora do núcleo.
O primeiro -quantum () será emitido isotopicamente. A detecção desse quantum em um detector seleciona um subconjunto com uma orientação das muitas direções possíveis que tem um dado. O segundo-quantum () tem uma emissão anisotrópica e mostra o efeito da correlação angular. O objetivo é medir a probabilidade relativa com a detecção de no ângulo fixo em relação a . A probabilidade é dada com a correlação do ângulo ( teoria das perturbações ):
Para --cascata, é devido à preservação da paridade :
Onde é o spin do estado intermediário e com a multipolaridade [ desambiguação necessária ] das duas transições. Para transições multipolares puras, é.
é o coeficiente de anisotropia que depende do momento angular do estado intermediário e das multipolaridades da transição.
O núcleo radioativo é construído no material da amostra e emite dois -quanta após a decadência. Durante a vida do estado intermediário, ou seja, o tempo entre e , o núcleo sofre uma perturbação devido à interação hiperfina por meio de seu ambiente elétrico e magnético. Este distúrbio muda a correlação angular para:
é o fator de perturbação. Devido à interação elétrica e magnética, o momento angular do estado intermediárioexperimenta um torque em torno de seu eixo de simetria. Mecanicamente quântico, isso significa que a interação leva a transições entre os M estados. O segundo-quantum () é então enviado do nível intermediário. Essa mudança populacional é a razão para a atenuação da correlação.
A interação ocorre entre o momento dipolar do núcleo magnético e o estado intermediário ou / e um campo magnético externo . A interação também ocorre entre o momento quadrupolo nuclear e o gradiente de campo elétrico fora do núcleo.
Dipolo magnético interação [ editar ]
Para a interação do dipolo magnético, a frequência da precessão do spin nuclear em torno do eixo do campo magnético É dado por:
é o fator g Landé eé o magneto nuclear .
Com segue:
Da teoria geral, obtemos:
Para a interação magnética segue:
Para a interação do dipolo magnético, a frequência da precessão do spin nuclear em torno do eixo do campo magnético É dado por:
é o fator g Landé eé o magneto nuclear .
Com segue:
Da teoria geral, obtemos:
Para a interação magnética segue:
Estática quadrupolo interação elétrica [ editar ]
A energia da interação elétrica hiperfina entre a distribuição de carga do núcleo e o campo elétrico estático extranuclear pode ser estendida a multipolares. O termo monopolo apenas causa uma mudança de energia e o termo dipolo desaparece, de modo que o primeiro termo de expansão relevante é o termo quadrupolo:
- ij = 1; 2; 3
Isso pode ser escrito como um produto do momento quadrupolo e o gradiente do campo elétrico . Ambos os [tensores] são de segunda ordem. Ordens mais altas têm efeito muito pequeno para serem medidas com PAC.
O gradiente do campo elétrico é a segunda derivada do potencial elétrico no centro:
torna-se diagonalizado, que:
A matriz está livre de traços no sistema de eixo principal ( equação de Laplace )
Normalmente, o gradiente do campo elétrico é definido com a maior proporção e :
- ,
Em cristais cúbicos, os parâmetros do eixo da célula unitária x, y, z têm o mesmo comprimento. Portanto:
- e
Em sistemas axissimétricos é .
Para gradientes de campo elétrico axialmente simétricos, a energia dos subestados tem os valores:
A diferença de energia entre dois subestados, e , É dado por:
A frequência quadrupolar é introduzido. As fórmulas nos quadros coloridos são importantes para a avaliação:
A maioria das publicações lista . como carga elementar ecomo constantes de Planck são bem conhecidas ou bem definidas. O momento quadrupolo nuclear é frequentemente determinado apenas de forma muito imprecisa (frequentemente apenas com 2-3 dígitos). Porque pode ser determinado com muito mais precisão do que , não é útil especificar apenas por causa da propagação do erro. Além do que, além do mais,é independente do giro! Isso significa que as medições de dois isótopos diferentes do mesmo elemento podem ser comparadas, como 199m Hg (5 / 2−), 197m Hg (5 / 2−) e 201m Hg (9 / 2−). Mais longe, pode ser usado como método de impressão digital.
Para a diferença de energia, segue:
E se , então:
com:
Para rotações inteiras aplica-se:
- und
Para giros de meio inteiro aplica-se:
- und
O fator de perturbação é dado por:
Com o fator para as probabilidades das frequências observadas:
No que diz respeito à interação dipolo magnética, a interação quadrupolo elétrica também induz uma precisão da correlação angular no tempo e isso modula a frequência de interação quadrupolar. Esta frequência é uma sobreposição das diferentes frequências de transição. As amplitudes relativas dos vários componentes dependem da orientação do gradiente de campo elétrico em relação aos detectores (eixo de simetria) e do parâmetro de assimetria. Para uma sonda com diferentes núcleos de sonda, é necessário um parâmetro que permita uma comparação direta: Portanto, a constante de acoplamento quadrupolo independente do spin nuclear é introduzido.
A energia da interação elétrica hiperfina entre a distribuição de carga do núcleo e o campo elétrico estático extranuclear pode ser estendida a multipolares. O termo monopolo apenas causa uma mudança de energia e o termo dipolo desaparece, de modo que o primeiro termo de expansão relevante é o termo quadrupolo:
- ij = 1; 2; 3
Isso pode ser escrito como um produto do momento quadrupolo e o gradiente do campo elétrico . Ambos os [tensores] são de segunda ordem. Ordens mais altas têm efeito muito pequeno para serem medidas com PAC.
O gradiente do campo elétrico é a segunda derivada do potencial elétrico no centro:
torna-se diagonalizado, que:
A matriz está livre de traços no sistema de eixo principal ( equação de Laplace )
Normalmente, o gradiente do campo elétrico é definido com a maior proporção e :
- ,
Em cristais cúbicos, os parâmetros do eixo da célula unitária x, y, z têm o mesmo comprimento. Portanto:
- e
Em sistemas axissimétricos é .
Para gradientes de campo elétrico axialmente simétricos, a energia dos subestados tem os valores:
A diferença de energia entre dois subestados, e , É dado por:
A frequência quadrupolar é introduzido. As fórmulas nos quadros coloridos são importantes para a avaliação:
A maioria das publicações lista . como carga elementar ecomo constantes de Planck são bem conhecidas ou bem definidas. O momento quadrupolo nuclear é frequentemente determinado apenas de forma muito imprecisa (frequentemente apenas com 2-3 dígitos). Porque pode ser determinado com muito mais precisão do que , não é útil especificar apenas por causa da propagação do erro. Além do que, além do mais,é independente do giro! Isso significa que as medições de dois isótopos diferentes do mesmo elemento podem ser comparadas, como 199m Hg (5 / 2−), 197m Hg (5 / 2−) e 201m Hg (9 / 2−). Mais longe, pode ser usado como método de impressão digital.
Para a diferença de energia, segue:
E se , então:
com:
Para rotações inteiras aplica-se:
- und
Para giros de meio inteiro aplica-se:
- und
O fator de perturbação é dado por:
Com o fator para as probabilidades das frequências observadas:
No que diz respeito à interação dipolo magnética, a interação quadrupolo elétrica também induz uma precisão da correlação angular no tempo e isso modula a frequência de interação quadrupolar. Esta frequência é uma sobreposição das diferentes frequências de transição. As amplitudes relativas dos vários componentes dependem da orientação do gradiente de campo elétrico em relação aos detectores (eixo de simetria) e do parâmetro de assimetria. Para uma sonda com diferentes núcleos de sonda, é necessário um parâmetro que permita uma comparação direta: Portanto, a constante de acoplamento quadrupolo independente do spin nuclear é introduzido.
Interações combinadas [ editar ]
Se houver uma interação magnética e elétrica ao mesmo tempo no núcleo radioativo, conforme descrito acima, resultarão em interações combinadas. Isso leva à divisão das frequências respectivamente observadas. A análise pode não ser trivial devido ao maior número de frequências que devem ser alocadas. Estes dependem, em cada caso, da direção dos campos elétrico e magnético entre si no cristal. O PAC é uma das poucas maneiras pelas quais essas direções podem ser determinadas.
Se houver uma interação magnética e elétrica ao mesmo tempo no núcleo radioativo, conforme descrito acima, resultarão em interações combinadas. Isso leva à divisão das frequências respectivamente observadas. A análise pode não ser trivial devido ao maior número de frequências que devem ser alocadas. Estes dependem, em cada caso, da direção dos campos elétrico e magnético entre si no cristal. O PAC é uma das poucas maneiras pelas quais essas direções podem ser determinadas.
Interações dinâmicas [ editar ]
Se o campo hiperfino flutua durante a vida do nível intermediário devido a saltos da sonda para outra posição da rede ou de saltos de um átomo próximo para outra posição da rede, a correlação é perdida. Para o caso simples com uma rede não distorcida de simetria cúbica, para uma taxa de salto de para lugares equivalentes , um amortecimento exponencial da estática -termos é observado:
-
Aqui é uma constante a ser determinada, que não deve ser confundida com a constante de decaimento . Para grandes valores de, apenas o decaimento exponencial puro pode ser observado:
O caso limite após Abragam-Pound é , E se , então:
Se o campo hiperfino flutua durante a vida do nível intermediário devido a saltos da sonda para outra posição da rede ou de saltos de um átomo próximo para outra posição da rede, a correlação é perdida. Para o caso simples com uma rede não distorcida de simetria cúbica, para uma taxa de salto de para lugares equivalentes , um amortecimento exponencial da estática -termos é observado:
Aqui é uma constante a ser determinada, que não deve ser confundida com a constante de decaimento . Para grandes valores de, apenas o decaimento exponencial puro pode ser observado:
O caso limite após Abragam-Pound é , E se , então:
Efeitos posteriores [ editar ]
Núcleos que transmutam antes do --cascade geralmente causa uma mudança de carga em cristais iônicos (In 3+ ) para Cd 2+ ). Como resultado, a rede deve responder a essas mudanças. Defeitos ou íons vizinhos também podem migrar. Da mesma forma, o processo de transição de alta energia pode causar o efeito Auger , que pode levar o núcleo a estados de ionização mais elevados. A normalização do estado de carga então depende da condutividade do material. Nos metais, o processo ocorre muito rapidamente. Isso leva muito mais tempo em semicondutores e isoladores. Em todos esses processos, o campo hiperfino muda. Se essa mudança cair dentro do--cascade, pode ser observado como um efeito colateral.
O número de núcleos no estado (a) na imagem à direita é despovoado pela decadência após o estado (b) e após o estado (c):
mit:
Disto obtém-se o caso exponencial:
Para o número total de núcleos no estado estático (c) segue:
As probabilidades iniciais de ocupação são para ambientes estáticos e dinâmicos:
Núcleos que transmutam antes do --cascade geralmente causa uma mudança de carga em cristais iônicos (In 3+ ) para Cd 2+ ). Como resultado, a rede deve responder a essas mudanças. Defeitos ou íons vizinhos também podem migrar. Da mesma forma, o processo de transição de alta energia pode causar o efeito Auger , que pode levar o núcleo a estados de ionização mais elevados. A normalização do estado de carga então depende da condutividade do material. Nos metais, o processo ocorre muito rapidamente. Isso leva muito mais tempo em semicondutores e isoladores. Em todos esses processos, o campo hiperfino muda. Se essa mudança cair dentro do--cascade, pode ser observado como um efeito colateral.
O número de núcleos no estado (a) na imagem à direita é despovoado pela decadência após o estado (b) e após o estado (c):
mit:
Disto obtém-se o caso exponencial:
Para o número total de núcleos no estado estático (c) segue:
As probabilidades iniciais de ocupação são para ambientes estáticos e dinâmicos:
Teoria geral [ editar ]
Na teoria geral para uma transição é dada:
- Von mínimo
com:
Na teoria geral para uma transição é dada:
- Von mínimo
com:
Referências
Em física quântica, a regra de ouro de Fermi expressa a taxa de transição (probabilidade por unidade de tempo) de um auto-estado de um Hamiltoniano para um contínuo de estados, devido a uma perturbação , que pode depender do tempo. Seu nome é uma homenagem ao físico italiano Enrico Fermi.
Dado um auto-estado do Hamiltoniano não perturbado , a probabilidade de transição para um estado é dado em primeira ordem de teoria de perturbação por
sendo a densidade de estados finais.
Em física estatística e física da matéria condensada, densidade de estados (DOS, do inglês density of states) é a propriedade que quantifica quão proximamente "empacotado" em níveis de energia está um sistema mecânico quântico. Um DOS alto em um nível específico de energia significa que há muitos estados disponíveis para ocupação. Um DOS nulo, zero, significa que nenhum estado pode ser ocupado em um nível de energia.
Em física quântica, a regra de ouro de Fermi expressa a taxa de transição (probabilidade por unidade de tempo) de um auto-estado de um Hamiltoniano para um contínuo de estados, devido a uma perturbação , que pode depender do tempo. Seu nome é uma homenagem ao físico italiano Enrico Fermi.
Dado um auto-estado do Hamiltoniano não perturbado , a probabilidade de transição para um estado é dado em primeira ordem de teoria de perturbação por
sendo a densidade de estados finais.
Em física estatística e física da matéria condensada, densidade de estados (DOS, do inglês density of states) é a propriedade que quantifica quão proximamente "empacotado" em níveis de energia está um sistema mecânico quântico. Um DOS alto em um nível específico de energia significa que há muitos estados disponíveis para ocupação. Um DOS nulo, zero, significa que nenhum estado pode ser ocupado em um nível de energia.
Índice
Explanação
Ondas, partículas comportando-se como ondas, podem somente existir dentro de sistemas mecânico quânticos (MQ) se propriedades do sistema seguem a ondulação existente. Em alguns sistemas, o espaçamento interatômico e a carga atômica do material segue somente elétrons de certos comprimento de onda existentes. Em outros sistemas. a estrutura cristalina do material leva ondas a se propagar em somente uma direção, enquanto suprime a propagação de ondas em outra direção. Ondas em um sistema MQ tem comprimentos de onda específicos e podem propagar-se em direções específicas, e cada onda ocupa um diferente modo,ou estado. Devido a muitos destes estados terem o mesmos comprimentos de onda, entretanto dividirem a mesma energia, podem existir muitos estados disponíveis em certos níveis de energia, enquanto nenhum estado é disponível em outros níveis de energia.
Por exemplo, a densidade de estados para elétrons em um semicondutor é mostrada em vermelho na Fig. 2. Para elétrons na fronteira da faixa de condução, muito poucos estados estão disponíveis para o elétron ocupar. A medida que o elétron aumenta em energia, a densidade de estados do elétron aumenta e mais estados tornam-se disponíveis para ocupação. Entretanto, porque não há estados disponíveis para elétrons ocuparem dentro da faixa de abertura, elétrons na fronteira da faixa de condução devem perder pelo menos de energia de maneira a realizarem a transição a outro estado disponível.
A densidade de estados pode ser calculada para elétrons, fótons, ou fónons em sistemas MQ. É usualmente notado com um dos símbolos g, , n, ou N. É uma função g(E) da energia interna E, na qual a expressão g(E) dE representa o número de estado com energias entre E e E+dE.
Para converter entre energia e vetor de onda, a relação específica entre E e k deve ser conhecida. Por exemplo, a fórmula para elétrons é
E para fótons, a fórmula é
Pode também ser escrito como uma função da frequência angular , a qual é proporcional à energia. A densidade de estados é usada extensivamente em física da matéria condensada, onde pode referir-se ao nível de energia dos elétrons, fótons ou fônons em um sólido cristalino. Em sólidos cristalinos, há frequentemente níveis de energia onde a densidade dos estados dos elétrons é zero, o que significa que os elétrons não podem ser excitados a estas energias. A densidade dos estados também ocorre na regra dourada de Fermi, a qual descreve quão rápido as transições mecânico quânticas ocorrem na presença de uma perturbação.
Num sistema tridimensional, a densidade de estados em espaço recíproco (espaço k) é
onde V é o volume e n o número de pontos de ramificação que existem para um único valor de k. Estes pontos de ramificação são por exemplo o spin-acima e spin-abaixo estados para elétrons, as polarizações de fótons, e os modos longitudinais ou transversais para fônons.
Ondas, partículas comportando-se como ondas, podem somente existir dentro de sistemas mecânico quânticos (MQ) se propriedades do sistema seguem a ondulação existente. Em alguns sistemas, o espaçamento interatômico e a carga atômica do material segue somente elétrons de certos comprimento de onda existentes. Em outros sistemas. a estrutura cristalina do material leva ondas a se propagar em somente uma direção, enquanto suprime a propagação de ondas em outra direção. Ondas em um sistema MQ tem comprimentos de onda específicos e podem propagar-se em direções específicas, e cada onda ocupa um diferente modo,ou estado. Devido a muitos destes estados terem o mesmos comprimentos de onda, entretanto dividirem a mesma energia, podem existir muitos estados disponíveis em certos níveis de energia, enquanto nenhum estado é disponível em outros níveis de energia.
Por exemplo, a densidade de estados para elétrons em um semicondutor é mostrada em vermelho na Fig. 2. Para elétrons na fronteira da faixa de condução, muito poucos estados estão disponíveis para o elétron ocupar. A medida que o elétron aumenta em energia, a densidade de estados do elétron aumenta e mais estados tornam-se disponíveis para ocupação. Entretanto, porque não há estados disponíveis para elétrons ocuparem dentro da faixa de abertura, elétrons na fronteira da faixa de condução devem perder pelo menos de energia de maneira a realizarem a transição a outro estado disponível.
A densidade de estados pode ser calculada para elétrons, fótons, ou fónons em sistemas MQ. É usualmente notado com um dos símbolos g, , n, ou N. É uma função g(E) da energia interna E, na qual a expressão g(E) dE representa o número de estado com energias entre E e E+dE.
Para converter entre energia e vetor de onda, a relação específica entre E e k deve ser conhecida. Por exemplo, a fórmula para elétrons é
E para fótons, a fórmula é
Pode também ser escrito como uma função da frequência angular , a qual é proporcional à energia. A densidade de estados é usada extensivamente em física da matéria condensada, onde pode referir-se ao nível de energia dos elétrons, fótons ou fônons em um sólido cristalino. Em sólidos cristalinos, há frequentemente níveis de energia onde a densidade dos estados dos elétrons é zero, o que significa que os elétrons não podem ser excitados a estas energias. A densidade dos estados também ocorre na regra dourada de Fermi, a qual descreve quão rápido as transições mecânico quânticas ocorrem na presença de uma perturbação.
Num sistema tridimensional, a densidade de estados em espaço recíproco (espaço k) é
onde V é o volume e n o número de pontos de ramificação que existem para um único valor de k. Estes pontos de ramificação são por exemplo o spin-acima e spin-abaixo estados para elétrons, as polarizações de fótons, e os modos longitudinais ou transversais para fônons.
Materiais cristalinos
Dado que em materiais (cristalinos), o número de escalas varia linearmente com o volume, uma diferente definição de densidade de estados é algumas vezes usada, na qual g(E) ou g(k) é o número de estados por unidade de energia (vetor onda) e por unidade de volume ou por unidade de célula da grade.
Em um material cristalino, onde os estados mecânico quânticos podem ser descritos em termos de seus vetores de onda k, a densidade dos estados como uma função de k é não dependente das propriedades do material. Das condições periódicas segue que em um volume arbitrário , somente vetores k são mantidos satisfazendo
onde são inteiros positivos ou negativos arbitrários. Usando
pode ser derivado que para uma matriz tridimensional o número de estados G(k) dk entre k e k+dk é
para um único caso.
Em sólidos, a relação entre E e k é geralmente muito complexa e dependente do material. Se a relação é conhecida, a expressão para a densidade dos estados é
A relação acima é somente significativa se a energia somente depende da manitude do vetor k.
Dado que em materiais (cristalinos), o número de escalas varia linearmente com o volume, uma diferente definição de densidade de estados é algumas vezes usada, na qual g(E) ou g(k) é o número de estados por unidade de energia (vetor onda) e por unidade de volume ou por unidade de célula da grade.
Em um material cristalino, onde os estados mecânico quânticos podem ser descritos em termos de seus vetores de onda k, a densidade dos estados como uma função de k é não dependente das propriedades do material. Das condições periódicas segue que em um volume arbitrário , somente vetores k são mantidos satisfazendo
onde são inteiros positivos ou negativos arbitrários. Usando
pode ser derivado que para uma matriz tridimensional o número de estados G(k) dk entre k e k+dk é
para um único caso.
Em sólidos, a relação entre E e k é geralmente muito complexa e dependente do material. Se a relação é conhecida, a expressão para a densidade dos estados é
A relação acima é somente significativa se a energia somente depende da manitude do vetor k.
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC].
 + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
 + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL ![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCK

 [ESTADO QUÂNTICO]
[ESTADO QUÂNTICO]













































































































 de energia de maneira a realizarem a transição a outro estado disponível.
de energia de maneira a realizarem a transição a outro estado disponível.










Comentários
Postar um comentário